Estimateurs biaisés : focus sur les indicateurs de dispersion

Introduction

Un des objectif d’une étude statistique est d’estimer des quantités (ex : moyenne, variance, écart-type, …) permettant de décrire une population afin d’en étudier les caractéristiques. Pour estimer ces quantités, il est nécessaire de définir des fonctions mathématiques qu’on appelle des estimateurs. Ces estimateurs sont ensuite appliqués sur les données d‘échantillons issus de la population d’étude. Ainsi, si on souhaite estimer l’âge moyen des patients d’une population d’étude (noté ), on utilise l’estimateur de la moyenne arithmétique, en notant X la variable aléatoire représentant l’âge des patients : 

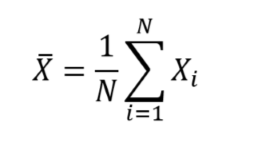
Estimation de la variance d’une variable aléatoire

Pour reprendre l’exemple précédent, imaginons que l’objectif soit d’estimer la variance de l’âge des patients dans la population. Pour ce faire, il est nécessaire de construire un estimateur de la variance. Une première proposition serait d’estimer de manière naïve la variance à l’aide de l’estimateur suivant :

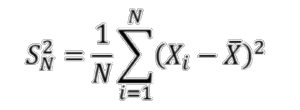
Il est possible de démontrer que cet estimateur est en réalité biaisé, malgré son apparence intuitive. On propose alors l’estimateur de la variance suivant :

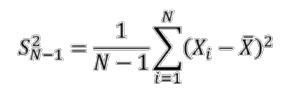
Il est possible de démontrer que cet estimateur est un estimateur sans biais de la variance de l’âge des patients dans la population d’étude*.

Pour illustrer cela, des simulations ont été effectuées. Le graphique suivant présente les estimations pour différentes tailles d’échantillon considérées.

Les résultats permettent de constater que pour des tailles d’échantillon faibles (inférieures ou égales à 10) le biais de l’estimateur naïf de la variance peut être assez élevé. En revanche pour des tailles d’échantillon plus importantes (supérieures ou égales à 100) le biais devient négligeable. L’estimateur corrigé de la variance est lui toujours sans biais, quelle que soit la taille d’échantillon considérée. La correction de l’estimateur n’étant pas complexe, il est bon de conserver cet estimateur corrigé, quelle que soit la taille d’échantillon considérée.

Estimation de l’écart-type d’une variable aléatoire

Il a été démontré précédemment que l’estimateur  était un estimateur non-biaisé de la variance d’une variable aléatoire. Pour estimer l’écart-type, il serait alors tentant de calculer . Il est cependant possible de démontrer que  est un estimateur biaisé de l’écart-type dans la population.

Il est également possible de démontrer que  devrait être un estimateur encore plus biaisé*.

Contrairement à l’estimateur de la variance, il est ici impossible de définir un estimateur de l’écart-type qui soit sans biais, quelle que soit la distribution de la variable X. En revanche, dans le cas où X suit une loi normale, il est possible d’exprimer le biais de . Il s’agit d’un biais multiplicatif noté  par convention*.

Ainsi, dans le cas où X suit une loi normale, il est possible de calculer l’estimateur sans biais suivant :

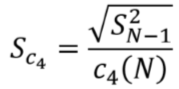
Pour illustrer les trois estimateurs de l’écart-type présentés ci-dessus, une étude de simulation similaire à la précédente a été menée. Le graphique suivant présente les estimations pour les différentes tailles d’échantillon considérées.

Les résultats permettent de constater que pour des tailles d’échantillon faibles (inférieures ou égales à 10) le biais de l’estimateur  peut être assez élevé. En revanche pour des tailles d’échantillon plus importantes (supérieures ou égales à 50) le biais devient négligeable. L’estimateur corrigé de l’écart-type (par la quantité ) est lui toujours sans biais, quelle que soit la taille d’échantillon considérée. Concernant l’estimateur , celui-ci n’a aucun intérêt car il est toujours plus biaisé que .

La correction de l’estimateur se fait au travers d’une quantité assez complexe (), c’est pour cela que l’estimateur biaisé de l’écart-type est conservé pour des tailles d’échantillons assez grandes, en revanche il est important d’apporter la correction pour des échantillons de petite taille.