Impact d’une transformation logarithmique de la variable de réponse dans un modèle ANCOVA

Différences entre moyenne arithmétique et moyenne géométrique

Avant d’aller plus loin dans cette thématique, il est important de faire un rappel sur ce que sont les moyennes arithmétiques et géométriques.

La moyenne arithmétique est la plus connue et la plus utilisée, quand on parle de « moyenne ». Elle se définit comme :

où X est une variable aléatoire quelconque.

La moyenne géométrique a également comme but de donner la tendance centrale d’une variable, mais au lieu d’utiliser la somme de cette variable, elle fait intervenir son produit :

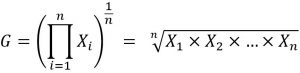
On peut également utiliser la formule suivante :

Il est possible de démontrer* que la moyenne géométrique G est toujours inférieure ou égale à la moyenne arithmétique A.

La deuxième expression de la moyenne géométrique est intéressante car il s’agit de la moyenne des valeurs de X à l’échelle logarithmique auxquelles on applique la fonction exponentielle. Cette expression nous sera utile par la suite, notamment pour comprendre l’impact d’une transformation logarithmique sur l’estimation de la moyenne d’une variable donnée.

A retenir : La moyenne géométrique est adaptée aux données biologiques qui suivent une loi log-normale. Elle est toujours inférieure ou égale à la moyenne arithmétique.

Impact d’une transformation logarithmique de base b de Y dans un modèle ANCOVA pour prédire la moyenne arithmétique de Y

L’objectif est de modéliser l’évolution d’une quantité quelconque (Y) sur k lots au cours du temps (T). Le modèle classiquement recommandé pour ce type d’analyse est un modèle de type ANCOVA exprimé de la manière suivante :

avec  le vecteur de paramètres des ordonnées à l’origine de chaque lot,

  le vecteur de paramètres de pentes de chaque lot et  l’erreur aléatoire du modèle sensé suivre une loi normale d’espérance 0 et de variance .

Lorsque l’hypothèse de normalité des résidus n’est pas respectée, il est classique de transformer la variable Y de telle sorte que Z = g(Y), avec g(.) la fonction de la transformation retenue, et d’ajuster un modèle identique sur la variable Z.

On prend ici le cas de la transformation logarithmique de base b de telle sorte que :

Dans ce cas, il est possible de modéliser Z à l’aide d’un modèle ANCOVA de la même manière que celle présentée précédemment :

avec . On note que dans cet exemple, la transformation logarithmique est appliquée seulement à Y et pas à la variable de temps T.

Une équation est calculée puis des prédictions de  (accompagnées de leurs intervalles de confiance) sont souvent calculées. Afin de les rendre exploitables scientifiquement, une transformation inverse est régulièrement appliquée afin de ramener les prédictions dans l’échelle initiale des données :

. Or, cette démarche introduit un biais dans les prédictions dont il faut être conscient et que l’on peut, ou non, accepter.

Explications : comme , il serait tentant d’appliquer cette même formule naïve à la prédiction moyenne de  à un temps donné (notée ), pour calculer la moyenne arithmétique de la prédiction de  (notée ). Cependant il est possible de démontrer* que cette formule est fausse quand elle est appliquée à la prédiction moyenne de . C’est-à-dire que :

En d’autre termes, la prédiction calculée avec les données sans transformation n’est pas égale à la prédiction du modèle sur les données transformées, après transformation inverse. En réalité,  correspond à la moyenne géométrique de la prédiction de , d’où la différence observée.

Si l’on souhaite calculer la moyenne arithmétique de la prédiction de  il est nécessaire d’utiliser la formule suivante* :

On en conclut que la formule naïve possède un biais multiplicatif noté  ce qui signifie que la formule naïve divise la vraie moyenne arithmétique par une quantité égale à . Ce biais multiplicatif est fonction :

• de b, la base de la transformation logarithmique effectuée,
• de 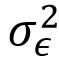,la variance résiduelle du modèle ajusté sur Z, la variable transformée en log. Pour rappel, 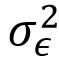mesure la variance qui n’est pas expliquée par le modèle (Mean Square Error). Théoriquement,  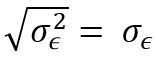devrait être du même ordre de grandeur que l’écart-type de la méthode de mesure.

Le graphique suivant montre la valeur du biais B en fonction de la variance résiduelle du modèle dans le cas d’une transformation logarithmique de base 10.

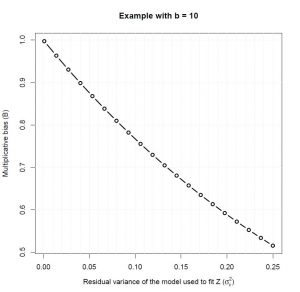
On constate sur ce graphique que plus la variance résiduelle est faible plus le biais est faible. Ainsi, si la variance résiduelle est faible (<0.025) alors le biais est assez faible dans l’estimation de la moyenne arithmétique via la formule naïve. En revanche, lorsque la variance résiduelle augmente, l’estimation de la moyenne arithmétique de  est grandement impactée. Par exemple, lorsque =0.25 alors l’estimation de la moyenne arithmétique de par la formule naïve est environ deux fois plus petite (B=1/0.5) que la vraie moyenne arithmétique.

Ainsi, lorsqu’une transformation a été appliquée pour des raisons pratiques (prérequis de l’ANCOVA non respectés) et que les données ne sont habituellement pas transformées, il est recommandé de tenir compte de ce biais même pour des variances résiduelles faibles ou d’exprimer les résultats des prédictions avec le modèle établi sur les données non transformées.

A retenir : appliquer une transformation inverse sur les prédictions d’un modèle traité en logarithme donne des « prédictions géométriques », et non des « prédictions arithmétiques ».